When you pour a glass of water, or fill a car with gasoline, you observe that water and gasoline flow freely. But when you pour syrup on pancakes or add oil to a car engine, you note that syrup and motor oil do not flow as readily. The viscosity of a liquid is a measure of its resistance to flow. Water, gasoline, and other liquids that flow freely have a low viscosity. Honey, syrup, motor oil, and other liquids that do not flow freely, like those shown in Figure \(\PageIndex\), have higher viscosities. We can measure viscosity by measuring the rate at which a metal ball falls through a liquid (the ball falls more slowly through a more viscous liquid) or by measuring the rate at which a liquid flows through a narrow tube (more viscous liquids flow more slowly).
The IMFs between the molecules of a liquid, the size and shape of the molecules, and the temperature determine how easily a liquid flows. As Table \(\PageIndex\) shows, the more structurally complex are the molecules in a liquid and the stronger the IMFs between them, the more difficult it is for them to move past each other and the greater is the viscosity of the liquid. As the temperature increases, the molecules move more rapidly and their kinetic energies are better able to overcome the forces that hold them together; thus, the viscosity of the liquid decreases.
| Substance | Formula | Viscosity (mPa·s) |
|---|---|---|
| water | H2O | 0.890 |
| mercury | Hg | 1.526 |
| ethanol | C2H5OH | 1.074 |
| octane | C8H18 | 0.508 |
| ethylene glycol | CH2(OH)CH2(OH) | 16.1 |
| honey | variable | ~2,000–10,000 |
| motor oil | variable | ~50–500 |
The various IMFs between identical molecules of a substance are examples of cohesive forces . The molecules within a liquid are surrounded by other molecules and are attracted equally in all directions by the cohesive forces within the liquid. However, the molecules on the surface of a liquid are attracted only by about one-half as many molecules. Because of the unbalanced molecular attractions on the surface molecules, liquids contract to form a shape that minimizes the number of molecules on the surface—that is, the shape with the minimum surface area. A small drop of liquid tends to assume a spherical shape, as shown in Figure \(\PageIndex\), because in a sphere, the ratio of surface area to volume is at a minimum. Larger drops are more greatly affected by gravity, air resistance, surface interactions, and so on, and as a result, are less spherical.
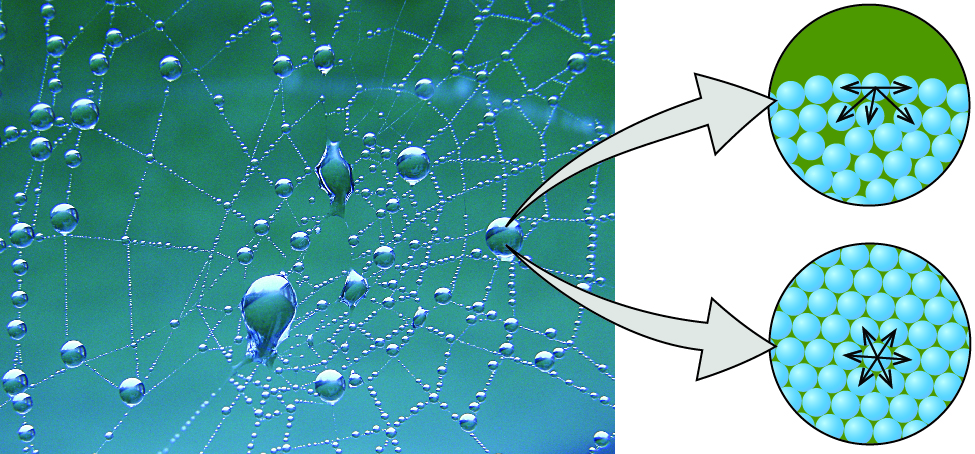bottom of a circular background. Five arrows are drawn pointing to the sides and downward from the sphere in the top middle of the drawing. The lower image shows another circular background of the same size as the first, but this time the blue spheres fill the image and are packed closely together. A sphere in the middle has six arrows pointing in all directions away from it." width="632px" height="294px" />
Surface tension is defined as the energy required to increase the surface area of a liquid, or the force required to increase the length of a liquid surface by a given amount. This property results from the cohesive forces between molecules at the surface of a liquid, and it causes the surface of a liquid to behave like a stretched rubber membrane. Surface tensions of several liquids are presented in Table \(\PageIndex\).
| Substance | Formula | Surface Tension (mN/m) |
|---|---|---|
| water | H2O | 71.99 |
| mercury | Hg | 458.48 |
| ethanol | C2H5OH | 21.97 |
| octane | C8H18 | 21.14 |
| ethylene glycol | CH2(OH)CH2(OH) | 47.99 |
Among common liquids, water exhibits a distinctly high surface tension due to strong hydrogen bonding between its molecules. As a result of this high surface tension, the surface of water represents a relatively “tough skin” that can withstand considerable force without breaking. A steel needle carefully placed on water will float. Some insects, like the one shown in Figure \(\PageIndex\), even though they are denser than water, move on its surface because they are supported by the surface tension.
The IMFs of attraction between two different molecules are called adhesive forces . Consider what happens when water comes into contact with some surface. If the adhesive forces between water molecules and the molecules of the surface are weak compared to the cohesive forces between the water molecules, the water does not “wet” the surface. For example, water does not wet waxed surfaces or many plastics such as polyethylene. Water forms drops on these surfaces because the cohesive forces within the drops are greater than the adhesive forces between the water and the plastic. Water spreads out on glass because the adhesive force between water and glass is greater than the cohesive forces within the water. When water is confined in a glass tube, its meniscus (surface) has a concave shape because the water wets the glass and creeps up the side of the tube. On the other hand, the cohesive forces between mercury atoms are much greater than the adhesive forces between mercury and glass. Mercury therefore does not wet glass, and it forms a convex meniscus when confined in a tube because the cohesive forces within the mercury tend to draw it into a drop (Figure \(\PageIndex\)).
If you place one end of a paper towel in spilled wine, as shown in Figure \(\PageIndex\), the liquid wicks up the paper towel. A similar process occurs in a cloth towel when you use it to dry off after a shower. These are examples of capillary action —when a liquid flows within a porous material due to the attraction of the liquid molecules to the surface of the material and to other liquid molecules. The adhesive forces between the liquid and the porous material, combined with the cohesive forces within the liquid, may be strong enough to move the liquid upward against gravity.
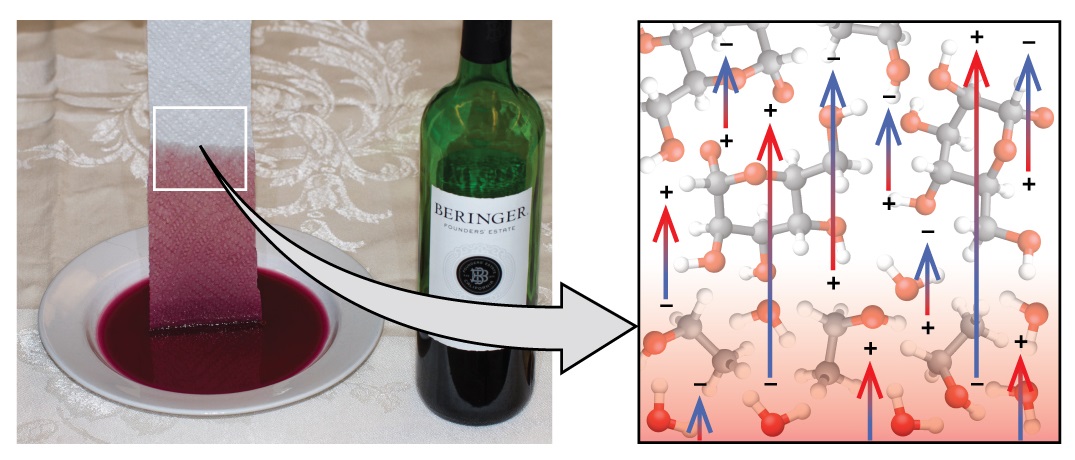
Towels soak up liquids like water because the fibers of a towel are made of molecules that are attracted to water molecules. Most cloth towels are made of cotton, and paper towels are generally made from paper pulp. Both consist of long molecules of cellulose that contain many −OH groups. Water molecules are attracted to these −OH groups and form hydrogen bonds with them, which draws the H2O molecules up the cellulose molecules. The water molecules are also attracted to each other, so large amounts of water are drawn up the cellulose fibers.
Capillary action can also occur when one end of a small diameter tube is immersed in a liquid, as illustrated in Figure \(\PageIndex\). If the liquid molecules are strongly attracted to the tube molecules, the liquid creeps up the inside of the tube until the weight of the liquid and the adhesive forces are in balance. The smaller the diameter of the tube is, the higher the liquid climbs. It is partly by capillary action occurring in plant cells called xylem that water and dissolved nutrients are brought from the soil up through the roots and into a plant. Capillary action is the basis for thin layer chromatography, a laboratory technique commonly used to separate small quantities of mixtures. You depend on a constant supply of tears to keep your eyes lubricated and on capillary action to pump tear fluid away.
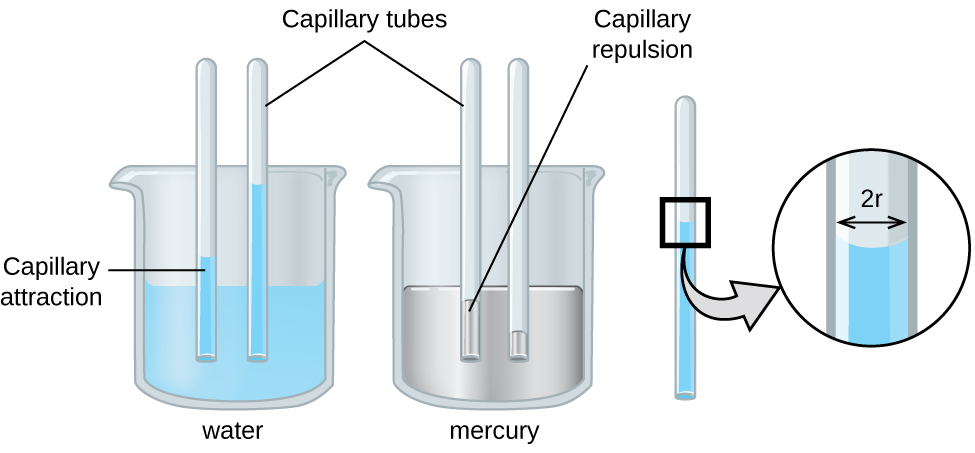in this image." width="539" height="250" />
The height to which a liquid will rise in a capillary tube is determined by several factors. The strength of attraction between particles in the liquid effects the surface tension. The surface tension and gravity compete with the attraction of the liquid to the container, the contact angle between them, the inner radius of the container, and the density of the liquid. When the tube is made of a material to which the liquid molecules are strongly attracted, they will spread out completely on the surface, which corresponds to a contact angle of 0°. This is the situation for water rising in a glass tube.
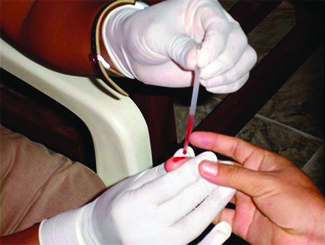
Many medical tests require drawing a small amount of blood, for example to determine the amount of glucose in someone with diabetes or the hematocrit level in an athlete. This procedure can be easily done because of capillary action, the ability of a liquid to flow up a small tube against gravity, as shown in Figure \(\PageIndex\). When your finger is pricked, a drop of blood forms and holds together due to surface tension—the unbalanced intermolecular attractions at the surface of the drop. Then, when the open end of a narrow-diameter glass tube touches the drop of blood, the adhesive forces between the molecules in the blood and those at the glass surface draw the blood up the tube. How far the blood goes up the tube depends on the diameter of the tube (and the type of fluid). A small tube has a relatively large surface area for a given volume of blood, which results in larger (relative) attractive forces, allowing the blood to be drawn farther up the tube. The liquid itself is held together by its own cohesive forces. When the weight of the liquid in the tube generates a downward force equal to the upward force associated with capillary action, the liquid stops rising.
Because the molecules of a liquid are in constant motion, we can plot the fraction of molecules with a given kinetic energy (KE) against their kinetic energy to obtain the kinetic energy distribution of the molecules in the liquid (Figure 7.8.8), just as we did for a gas. As for gases, increasing the temperature increases both the average kinetic energy of the particles in a liquid and the range of kinetic energy of the individual molecules. If we assume that a minimum amount of energy (E0) is needed to overcome the intermolecular attractive forces that hold a liquid together, then some fraction of molecules in the liquid always has a kinetic energy greater than E0. The fraction of molecules with a kinetic energy greater than this minimum value increases with increasing temperature. Any molecule with a kinetic energy greater than E0 has enough energy to overcome the forces holding it in the liquid and escape into the vapor phase. Before it can do so, however, a molecule must also be at the surface of the liquid, where it is physically possible for it to leave the liquid surface; that is, only molecules at the surface can undergo evaporation (or vaporization), where molecules gain sufficient energy to enter a gaseous state above a liquid’s surface, thereby creating a vapor pressure.
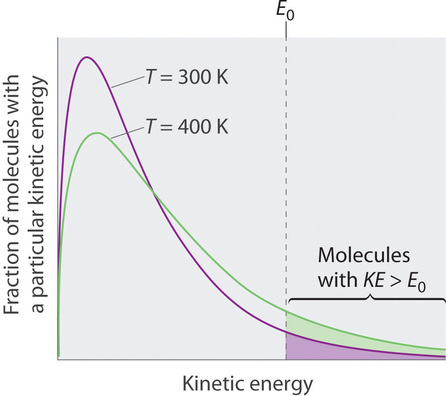
To understand the causes of vapor pressure, consider the apparatus shown in Figure 7.8.9. When a liquid is introduced into an evacuated chamber (part (a) in Figure 11.5.211.5.2), the initial pressure above the liquid is approximately zero because there are as yet no molecules in the vapor phase. Some molecules at the surface, however, will have sufficient kinetic energy to escape from the liquid and form a vapor, thus increasing the pressure inside the container. As long as the temperature of the liquid is held constant, the fraction of molecules with KE>E0KE>E0 will not change, and the rate at which molecules escape from the liquid into the vapor phase will depend only on the surface area of the liquid phase.
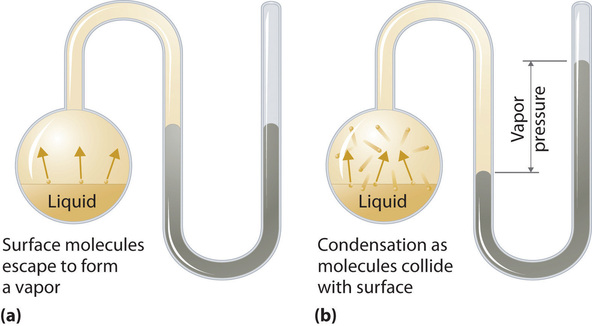
As soon as some vapor has formed, a fraction of the molecules in the vapor phase will collide with the surface of the liquid and reenter the liquid phase in a process known as condensation (part (b) in Figure 7.8.9). As the number of molecules in the vapor phase increases, the number of collisions between vapor-phase molecules and the surface will also increase. Eventually, a steady state will be reached in which exactly as many molecules per unit time leave the surface of the liquid (vaporize) as collide with it (condense). At this point, the pressure over the liquid stops increasing and remains constant at a particular value that is characteristic of the liquid at a given temperature. The rates of evaporation and condensation over time for a system such as this are shown graphically in Figure 7.8.10.
Two opposing processes (such as evaporation and condensation) that occur at the same rate and thus produce no net change in a system, constitute a dynamic equilibrium. In the case of a liquid enclosed in a chamber, the molecules continuously evaporate and condense, but the amounts of liquid and vapor do not change with time. The pressure exerted by a vapor in dynamic equilibrium with a liquid is the equilibrium vapor pressure of the liquid.
If a liquid is in an open container, however, most of the molecules that escape into the vapor phase will not collide with the surface of the liquid and return to the liquid phase. Instead, they will diffuse through the gas phase away from the container, and an equilibrium will never be established. Under these conditions, the liquid will continue to evaporate until it has “disappeared.” The speed with which this occurs depends on the vapor pressure of the liquid and the temperature. Volatile liquids have relatively high vapor pressures and tend to evaporate readily; nonvolatile liquids have low vapor pressures and evaporate more slowly. Although the dividing line between volatile and nonvolatile liquids is not clear-cut, as a general guideline, we can say that substances with vapor pressures greater than that of water (Figure 11.5.411.5.4) are relatively volatile, whereas those with vapor pressures less than that of water are relatively nonvolatile. Thus diethyl ether (ethyl ether), acetone, and gasoline are volatile, but mercury, ethylene glycol, and motor oil are nonvolatile.
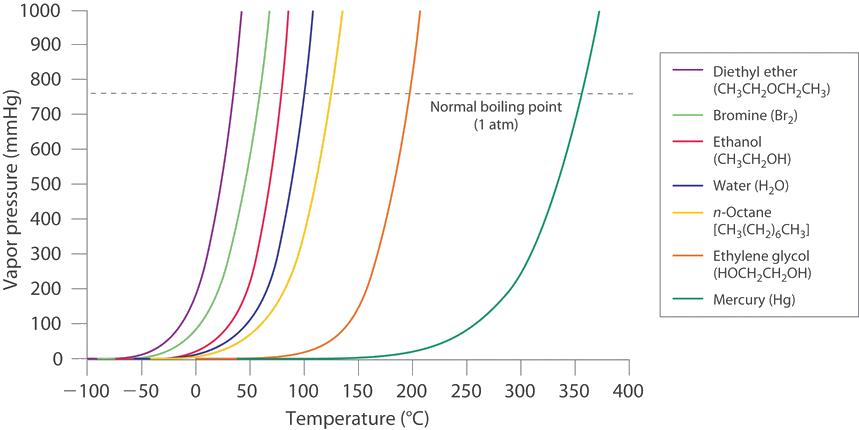
The equilibrium vapor pressure of a substance at a particular temperature is a characteristic of the material, like its molecular mass, melting point, and boiling point. It does not depend on the amount of liquid as long as at least a tiny amount of liquid is present in equilibrium with the vapor. The equilibrium vapor pressure does, however, depend very strongly on the temperature and the intermolecular forces present, as shown for several substances in Figure 11.5.411.5.4. Molecules that can hydrogen bond, such as ethylene glycol, have a much lower equilibrium vapor pressure than those that cannot, such as octane. The nonlinear increase in vapor pressure with increasing temperature is much steeper than the increase in pressure expected for an ideal gas over the corresponding temperature range. The temperature dependence is so strong because the vapor pressure depends on the fraction of molecules that have a kinetic energy greater than that needed to escape from the liquid, and this fraction increases exponentially with temperature. As a result, sealed containers of volatile liquids are potential bombs if subjected to large increases in temperature. The gas tanks on automobiles are vented, for example, so that a car won’t explode when parked in the sun. Similarly, the small cans (1–5 gallons) used to transport gasoline are required by law to have a pop-off pressure release.
Volatile substances have low boiling points and relatively weak intermolecular interactions; nonvolatile substances have high boiling points and relatively strong intermolecular interactions.
A Video Discussing Vapor Pressure and Boiling Points. Video Source: https://youtu.be/4QtcdpfRO1M
As the temperature of a liquid increases, the vapor pressure of the liquid increases until it equals the external pressure, or the atmospheric pressure in the case of an open container. Bubbles of vapor begin to form throughout the liquid, and the liquid begins to boil. The temperature at which a liquid boils at exactly 1 atm pressure is the normal boiling point of the liquid. For water, the normal boiling point is exactly 100°C. The normal boiling points of the other liquids in Figure 11.5.411.5.4 are represented by the points at which the vapor pressure curves cross the line corresponding to a pressure of 1 atm. Although we usually cite the normal boiling point of a liquid, the actual boiling point depends on the pressure. At a pressure greater than 1 atm, water boils at a temperature greater than 100°C because the increased pressure forces vapor molecules above the surface to condense. Hence the molecules must have greater kinetic energy to escape from the surface. Conversely, at pressures less than 1 atm, water boils below 100°C.
| Place | Altitude above Sea Level (ft) | Atmospheric Pressure (mmHg) | Boiling Point of Water (°C) |
|---|---|---|---|
| Mt. Everest, Nepal/Tibet | 29,028 | 240 | 70 |
| Bogota, Colombia | 11,490 | 495 | 88 |
| Denver, Colorado | 5280 | 633 | 95 |
| Washington, DC | 25 | 759 | 100 |
| Dead Sea, Israel/Jordan | −1312 | 799 | 101.4 |
Typical variations in atmospheric pressure at sea level are relatively small, causing only minor changes in the boiling point of water. For example, the highest recorded atmospheric pressure at sea level is 813 mmHg, recorded during a Siberian winter; the lowest sea-level pressure ever measured was 658 mmHg in a Pacific typhoon. At these pressures, the boiling point of water changes minimally, to 102°C and 96°C, respectively. At high altitudes, on the other hand, the dependence of the boiling point of water on pressure becomes significant. Table 11.5.111.5.1 lists the boiling points of water at several locations with different altitudes. At an elevation of only 5000 ft, for example, the boiling point of water is already lower than the lowest ever recorded at sea level. The lower boiling point of water has major consequences for cooking everything from soft-boiled eggs (a “three-minute egg” may well take four or more minutes in the Rockies and even longer in the Himalayas) to cakes (cake mixes are often sold with separate high-altitude instructions). Conversely, pressure cookers, which have a seal that allows the pressure inside them to exceed 1 atm, are used to cook food more rapidly by raising the boiling point of water and thus the temperature at which the food is being cooked.
As pressure increases, the boiling point of a liquid increases and vice versa.
Use Figure 11.5.411.5.4 to estimate the following.
1. the boiling point of water in a pressure cooker operating at 1000 mmHg
Given: Data in Figure 11.5.411.5.4, pressure, and boiling point
Asked for: corresponding boiling point and pressure
Strategy:
Solution:
Ethylene glycol is an organic compound primarily used as a raw material in the manufacture of polyester fibers and fabric industry, and polyethylene terephthalate resins (PET) used in bottling. Use the data in Figure 11.5.411.5.4 to estimate the following.
Answer b
The intermolecular forces between molecules in the liquid state vary depending upon their chemical identities and result in corresponding variations in various physical properties. Cohesive forces between like molecules are responsible for a liquid’s viscosity (resistance to flow) and surface tension (elasticity of a liquid surface). Adhesive forces between the molecules of a liquid and different molecules composing a surface in contact with the liquid are responsible for phenomena such as surface wetting and capillary rise. Because the molecules of a liquid are in constant motion and possess a wide range of kinetic energies, at any moment some fraction of them has enough energy to escape from the surface of the liquid to enter the gas or vapor phase. This process, called vaporization or evaporation, generates a vapor pressure above the liquid. Molecules in the gas phase can collide with the liquid surface and reenter the liquid via condensation. Eventually, a steady state is reached in which the number of molecules evaporating and condensing per unit time is the same, and the system is in a state of dynamic equilibrium. Under these conditions, a liquid exhibits a characteristic equilibrium vapor pressure that depends only on the temperature. Volatile liquids are liquids with high vapor pressures, which tend to evaporate readily from an open container; nonvolatile liquids have low vapor pressures. When the vapor pressure equals the external pressure, bubbles of vapor form within the liquid, and it boils. The temperature at which a substance boils at a pressure of 1 atm is its normal boiling point.
adhesive force force of attraction between molecules of different chemical identities capillary action flow of liquid within a porous material due to the attraction of the liquid molecules to the surface of the material and to other liquid molecules cohesive force force of attraction between identical molecules condensation change from a gaseous to a liquid state dynamic equilibrium state of a system in which reciprocal processes are occurring at equal rates evaporation change from a liquid to a gas state because of a fraction of molecules with a kinetic energy greater than the minimum value needed for phase change equilibrium vapor pressure pressure exerted by a vapor in equilibrium with a solid or a liquid at a given temperature nonvolative liquid liquid with a low vapor pressure, which tend to evaporate slowly from an open container normal boiling point temperature at which a liquid’s vapor pressure equals 1 atm (760 torr) surface tension energy required to increase the area, or length, of a liquid surface by a given amount vaporization change from liquid state to gaseous state vapor pressure pressure exerted by a vapor in a dynamic exchange with a solid or a liquid at a given temperature viscosity measure of a liquid’s resistance to flow volatile liquid liquid with a high vapor pressure, which tend to evaporate readily from an open container
This page titled 7.8: Properties of Liquids is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.
